欲望 快科技资讯2022年06月08日Blog版

素数的界说很简便欲望,小学生王人懂,但却有好多经典的数学未解之谜王人与它磋磨。
因此,素数在数论中的地位畸形遑急。
当今,一个跟它磋磨的猜想,就被26岁的牛津大学在读博士生给讲授了。

这是匈牙利数学家最早在1930年代提议来的一个对于原始集的问题。
由于小哥用到的王人是已有论点,许盛大学家王人被他的机灵重要惊到了。
具体是什么,通盘来看。
(前列一些高能预警。。)
来自1935年的猜想
开端,不知说念原始集(Primitive sets)这个主意全球熟不熟。
它和素数的界说差未几,指的是一组弗成相互被整除的数字的连合,比如{6,28,496,8128}。
天然,这些数王人要大于1。
由于素数只可被1和它自身整除,那么任何素数组成的连合就属于一种特殊的原始集。

△ 图源Quanta Magazine
原始集这个主意是由匈牙利数学家Paul Erd?s在1930年代提议的,最早仅仅用于讲授发源于古希腊的好意思满数。
天然它的界说很简便,但围绕着它也产生了一些很事理的属性。
比如你无法详情原始集到底有些许种组合,就比如在1-1000这些数中,占去一半数目的501-1000,拿出其中轻易几个数字王人不错组成一个原始集,因为它们王人无法被相互整除。
不外天然无法详情组合有多大,但Paul Erd?s发现对于任何原始集(包括无尽集),它的“Erd?s和”王人有上界,即小于或等于某个数字。
什么是“Erd?s和”?
即是对连合中的每个数字n求抒发式1/(n log n)的和,用公式抒发即是这样:
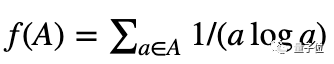
比如连合{2, 3, 55},它的“Erd?s和”就等于 1/(2 log 2) + 1/(3 log 3) + 1/(55 log 55)。
前边说到,“Erd?s和”是有界的,但咱们王人没法知说念最大的连合长什么样,这个界又缘何领悟呢?
尽管如斯,1988年,Erd?s如故给出了一个值,它猜测这个界为某个素数组成的原始集的和,为1.64。
这个猜想也把素数再次推上了“特立独行”的“风口浪尖”(这也即是标题里所说的“一个素数猜想”的具体含义了)。
几十年来欲望,数学家们在讲授这个猜想方面只得回了部分施展。
从大四战争到这个问题就被迷住了
牛津大学的博士生小哥Jared Duker Lichtman,从2018年运转战争到这个问题。
那会儿他如故达特茅斯学院的别称大四本科生。
他回忆称,我方一下子就被这个猜想迷住了:“这样奇怪的猜测奈何会是果然呢,太不可念念议了吧?”
成人电影网站于是接下来的四年间,从本科到牛津大学读博,小哥就跟这个猜想“杠”上了。
先讲授了不大于1.78
谁能猜想,2018年,他和他在达特茅斯学院的导师Carl Pomerance还真先通盘侧面讲授了原始集的“Erd?s和”不会大于1.78驾驭的猜想。
这个猜想是好意思国数学家弗兰兹·梅尔滕斯(Franz Mertens)提议来的。
他们算出这个常数的主义是先写下原始聚合每个数字的倍数,然后将每个序列中这些倍数进行领悟,出现了比面前原始数的最大质因数还要小的因数,就要丢掉。
然后将剩余的数字组成一个新连合。
举个具体例子。
假如原始集为{2, 3, 5},那么2的最大质因数是2,3的最大质因数是3,5的最大质因数是5。
通盘2的倍数全部及格,因为它们王人是2的公倍数,莫得突出2的质因数2;
通盘3的倍数中,唯有是素数2的公倍数(因为莫得突出质因数3),王人要被扔掉,也即是6、12、18王人分裂格;
通盘5的倍数中,唯有是素数2和3的公倍数(因为莫得突出质因数5),也要被pass,因此10、15、20、30分裂格;
再比如55的倍数中,唯有是素数2、3、5、7的公倍数,也要被pass,因为55的最大质因数为11。

△ 图源Quanta Magazine
牛津小哥将这种重要比作字典的索引形势,只不外字典是按字母,这是按素数来组织每个序列。
得到新的连合后,他和导师又运转算这些倍数序列的“密度”。就拿通盘偶数来说,它的序列“密度”即是为1/2,因为通盘偶数占通盘整数的一半。
然后啊,他们就不雅察到,若是给定的一个连合是原始集,那么通盘倍数序列就不会重复(overlap),因为他们的组合“密度”最多为1。
(为什么为1,因为整数的序列“密度”即是1。)
有了“密度”,就不错算连合的“Erd?s和”了,阐发弗兰兹·梅尔滕斯提议的定理,一个简略等于1.78的特殊常数乘以连合倍数的组合“密度”,就不错得出原始集的最大“Erd?s和”。
由于小哥和导师讲授连合的“密度”最大为1,也就从侧面讲授了“Erd?s和”的最大值为1.78。
小哥在牛津大学的导师对此赞扬有加,称小哥和原导师的重要其实是Paul Erd?s率先重要的一种变体,但它更精巧,得到了一个“not-tight”和“not-too-bad”的上界。
与此同期,全球以为他们的这个重要似乎一经是面前最顶尖的数学家才不错作念到的。
再讲授1.64
好,得胜了一小步,接下来怎样才气把规模削弱,讲授Erd?s给出的1.64呢?
小哥发现,他和前导师的那一套表面对于质因数较小的数字组成的原始集是有用的,不错相比豪恣地就讲授出来甚而比1.64还小的常数。
不外质因数大了就不太行。
左念念右想,转瞬到了博士三年齿,他发现不错给连合中的每个数字关联不啻一个倍数序列。
但和之前不异,通盘这些序列的组合密度最多为1。
比如对于618这个数字(2 x 3 × 103)来说,按照往时的重要不不错出现比103倍还小的倍数,但当今不错用比103倍还小的倍数组成序列,比如5倍。
(至于5倍如故几倍,这王人是有一套敛迹规定决定的。)
接着他又找到了一种更准确地算出这些序列的组合“密度”的重要。
最终,他仔细讨论了原始集的多样情况,在具有最大质因数和最小质因的数字之间找到了一个均衡,将2018年和当今的两部分讲授强迫在通盘,最终讲授了“Erd?s和”小于1.64。
前后一共花了四年的小哥示意,得出这个遵守不知说念是运说念好碰上了如故啥,总之作念到了。
详备讲授经由一经被他写成了论文发在了arXiv。

顽劣一番……的确是三行一个公式的情况。感兴味的数学大佬不错去望望。
非常学家指出,牛津小哥这个讲授遵守果然太引东说念主细心了,因为他的重要畸形机灵,富裕依赖于已有论点就作念到了。
与此同期,同业还示意,这一讲授肃肃了素数在原始连合中的特殊地位。
One More Thing
ps. 小哥有多锋利,不错从全球的响应侧面感受到。
就比如有网友通过小哥的个东说念主主页扒到他列出的最近出书物,发现从2018年到当今一共有至少18篇。

才读到博士就有这样多论文,这一数字让全球相配忌惮。
但有东说念主就站出来示意了:不及为奇,毕竟天才即是天才啊。(手动狗头)

论文地址:https://arxiv.org/abs/2202.02384
参考领路:[1]https://www.quantamagazine.org/graduate-students-side-project-proves-prime-number-conjecture-20220606/[2]https://news.ycombinator.com/item?id=31640297欲望
